8ª Hora Open Course

Para finalizar el curso se nos cuenta las propiedades de los números complejos y la formas en que se pueden presentar: forma binomica o forma polar.

Para cada número complejo z, la primera componente, x, se denomina parte real y la segunda, y, se denomina parte imaginaria.

Obviamente, dos números complejos son iguales si y sólo si lo son simultáneamente sus partes reales y sus partes imaginarias

Se define el módulo de un número complejo como el módulo del vector que lo representa, es decir, si 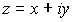, entonces el módulo de  es .

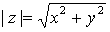El conjugado de un número complejo se define como su simétrico respecto del eje real, es decir, si 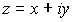, entonces el conjugado de  es .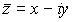

Otra forma de expresar un número complejo es la forma polar o forma módulo-argumento, donde 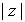es el módulo de , y donde q es un argumento de , esto es, q es un ángulo tal que

arctg= parte imaginaria /parte real 

Y finalmente  pasar este q a radianes para obteber la forma polar del numero complejo.