9ª Hora de Open Course

Ya finalizado este curso Open Course de matemáticas vamos a decir que a sido un curso que apesar de que los conocimientos ofrecidos ya eran conocidos, siempre viene bien refrescar la memoria y al final siempre se aprende algo nuevo.
El curso a sido realizado por la Universidad Politécnica de Valencia, en mi opinión la pagina y los temas eran muy fáciles de encontrar. Era bastante sencillo manejarse por la pagina web cosa que es de agradecer. También hay que recordar que al finalizar cada tema se nos presentaban una serie de cuestiones tipo test muy cortas que servían par afianzar los conocimientos.

8ª Hora Open Course

Para finalizar el curso se nos cuenta las propiedades de los números complejos y la formas en que se pueden presentar: forma binomica o forma polar.

Para cada número complejo z, la primera componente, x, se denomina parte real y la segunda, y, se denomina parte imaginaria.

Obviamente, dos números complejos son iguales si y sólo si lo son simultáneamente sus partes reales y sus partes imaginarias

Se define el módulo de un número complejo como el módulo del vector que lo representa, es decir, si 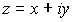, entonces el módulo de  es .

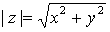El conjugado de un número complejo se define como su simétrico respecto del eje real, es decir, si 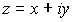, entonces el conjugado de  es .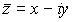

Otra forma de expresar un número complejo es la forma polar o forma módulo-argumento, donde 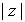es el módulo de , y donde q es un argumento de , esto es, q es un ángulo tal que

arctg= parte imaginaria /parte real 

Y finalmente  pasar este q a radianes para obteber la forma polar del numero complejo.

7ª Hora Open Course

Entramos en el ultimo tema del curso: LOS NÚMEROS COMPLEJOS 
(Mas vale prestar atención porque esta es una pregunta de examen).

El conjunto de los números complejos se designa como , siendo el conjunto de los reales se cumple que . Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i), o en forma polar.

Los números complejos son la herramienta de trabajo del álgebra, análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, aerodinámica y electromagnetismo entre otras de gran importancia. Además los números complejos se utilizan por doquier en matemáticas, en muchos campos de la física (notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.

6ª Hora Open Course

  

Cabe destacar en los vídeos de la unidad 1, la explicación de calculo de operaciones avanzadas como:

Las potencias















Las raíces



Y las igualdades notables




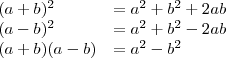
Estas serie de propiedades aran mucho mas rapidos nuestros calculos y nos ayudaran bastante en nuestros examenes asi que mas vale memorizarlas bien. :)

5ª Hora del Open Course

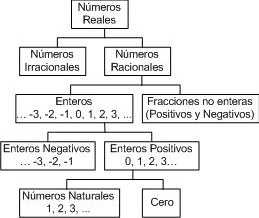
Las siguientes horas se nos enseñan la variedad de números que podemos encontrar en las matemáticas y sus conjuntos. Cabe destacar las operaciones matemáticas que se pueden realizar con ellos ya que por ejemplo los números irracionales no permiten las mismas características que los números enteros.
Se nos da un resumen de cada conjunto numérico y las propiedades que este tiene.

Es básico para las operaciones y cálculos que realizamos en esta asignatura y en muchos aspectos de la vida real.