9ª Hora de Open Course

Ya finalizado este curso Open Course de matemáticas vamos a decir que a sido un curso que apesar de que los conocimientos ofrecidos ya eran conocidos, siempre viene bien refrescar la memoria y al final siempre se aprende algo nuevo.
El curso a sido realizado por la Universidad Politécnica de Valencia, en mi opinión la pagina y los temas eran muy fáciles de encontrar. Era bastante sencillo manejarse por la pagina web cosa que es de agradecer. También hay que recordar que al finalizar cada tema se nos presentaban una serie de cuestiones tipo test muy cortas que servían par afianzar los conocimientos.

8ª Hora Open Course

Para finalizar el curso se nos cuenta las propiedades de los números complejos y la formas en que se pueden presentar: forma binomica o forma polar.

Para cada número complejo z, la primera componente, x, se denomina parte real y la segunda, y, se denomina parte imaginaria.

Obviamente, dos números complejos son iguales si y sólo si lo son simultáneamente sus partes reales y sus partes imaginarias

Se define el módulo de un número complejo como el módulo del vector que lo representa, es decir, si 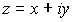, entonces el módulo de  es .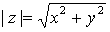

El conjugado de un número complejo se define como su simétrico respecto del eje real, es decir, si 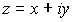, entonces el conjugado de  es .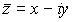

Otra forma de expresar un número complejo es la forma polar o forma módulo-argumento, donde es el módulo de , y donde q es un argumento de , esto es, q es un ángulo tal que

arctg= parte imaginaria /parte real 

Y finalmente  pasar este q a radianes para obteber la forma polar del numero complejo.

7ª Hora Open Course

Entramos en el ultimo tema del curso: LOS NÚMEROS COMPLEJOS 
(Mas vale prestar atención porque esta es una pregunta de examen).

El conjunto de los números complejos se designa como , siendo el conjunto de los reales se cumple que . Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i), o en forma polar.

Los números complejos son la herramienta de trabajo del álgebra, análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, aerodinámica y electromagnetismo entre otras de gran importancia. Además los números complejos se utilizan por doquier en matemáticas, en muchos campos de la física (notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.

6ª Hora Open Course

  

Cabe destacar en los vídeos de la unidad 1, la explicación de calculo de operaciones avanzadas como:

Las potencias















Las raíces



Y las igualdades notables




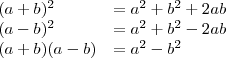
Estas serie de propiedades aran mucho mas rapidos nuestros calculos y nos ayudaran bastante en nuestros examenes asi que mas vale memorizarlas bien. :)

5ª Hora del Open Course

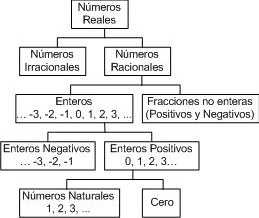
Las siguientes horas se nos enseñan la variedad de números que podemos encontrar en las matemáticas y sus conjuntos. Cabe destacar las operaciones matemáticas que se pueden realizar con ellos ya que por ejemplo los números irracionales no permiten las mismas características que los números enteros.
Se nos da un resumen de cada conjunto numérico y las propiedades que este tiene.

Es básico para las operaciones y cálculos que realizamos en esta asignatura y en muchos aspectos de la vida real.

4ª HORA DEL OPEN COURSE

En estos vídeos podemos destacar los ejemplos y operaciones con conjuntos. Si en un conjunto tenemos contenido otro conjunto, o cuales son los elementos que se repiten en ambos conjuntos y cuales son particulares de un solo conjunto.
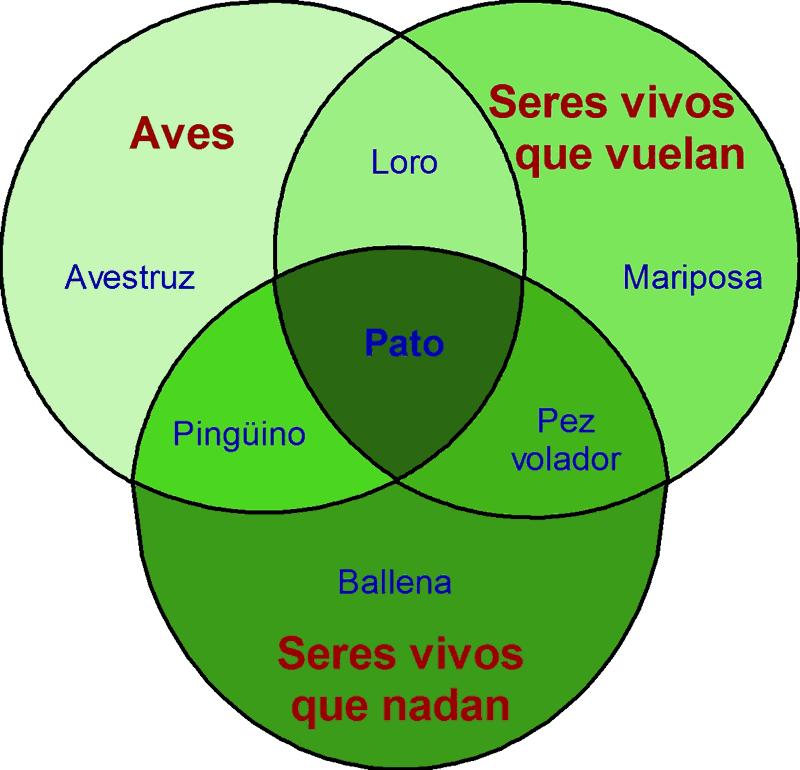
Todo esto lo podemos aprender de un forma muy gráfica con el diagrama de Venn una forma rápida y visual de los elementos que pertenecen a cada conjunto subconjunto y etc.

Como se muestra en la imagen podemos ver los animales tiene en común un tipo de propiedades ya que comparten una parte del circulo.

3ª HORA OPEN COURSE

En los siguientes videos se nos explica un poco de historia sobre los conjuntos, fueron creados por el matematico Cantor, tambien los tipos de conjuntos existentes:

- Enumeración: escribimos uno a uno cada uno de los elementos del conjunto. 

- Descripción: damos una descripción verbal o simbólica de los elementos.

Cabe destacar que los elementos de un conjunto no tienen  ningún orden preestablecido !!!! 

2º Hora del open course

En un comienzo se nos explica varios simbolos que sirven para expresar expresiones como:  Tal que, Para todo, etc. Estos simbolos junto con los de las siguientes lecciones, mayor que (<), menor (>)... Hacen de la simbologia algo muy importante en la matematica. Gracias a estos simbolos podemos abreviar nuestra forma de expresarnos matematicamente.



P.D: la foto esta en portugues pero mas o menos se entiende jajaja

1º Hora de Curso Open Course

Habiendo visto ya el curso online de la Universidad Politécnica de Valencia completo, podemos decir que es un curso instructivo para aquellas personas con poca base matemática. En el curso se nos da un breve y instructivo repaso sobre la terminología matemática, que nos ahorra "mucha literatura" juntamente con un pequeña explicación sobre los conjuntos numéricos y sus clasificaciones (natural, entero...) de manera bastante visual y fácil de entender. Por ultimo se nos presentan las operaciones básicas con números complejos.

Cabe añadir que después de cada ejercicio se nos presentan ejercicios interactivos tipo test dándonos las respuestas y viendo si hemos afianzado los conceptos.

3ª HORA SISTEMA DE NUMERACIÓN DECIMAL

Se llama decimal o de base diez porque se utilizan diez símbolos para 
representar todos los números. Los diez símbolos, cifras son: 

 0, 1, 2,3, 4, 5, 6, 7, 8, 9 

La relación decimal que hay entre las diversas unidades es: 

1 decena lo unidades 
1 centena = lo decenas 
1 millar = 10 centenas 
1 cent. de mil = 10 dec. de mil 
1 millón =-10 cent. de mil . 

Cada diez unidades de un orden cualquiera forman una unidad del 
orden inmediato superior. 

Excepto en ciertas culturas, es el sistema usado habitualmente en todo el mundo y en todas las áreas que requieren de un sistema de numeración. Sin embargo hay ciertas técnicas, como por ejemplo en la informática, donde se utilizan sistemas de numeración adaptados al método del binario o el hexadecimal.

Según los antropólogos, el origen del sistema decimal está en los diez dedos que tenemos los humanos en las manos, los cuales siempre nos han servido de base para contar.

También existen algunos vestigios del uso de otros sistemas de numeración, como el quinario, el duodecimal y el vigesimal.

SEGUNDA HORA DE OPEN COURSE

La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.

Sin embargo, la teoría de los conjuntos es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas,  y junto con la lógica permite estudiar los fundamentos de esta.

Además, la propia teoría de conjuntos es objeto de estudio  en particular las propiedades y relaciones de los conjuntos infinitos. En esta disciplina es habitual que se presenten casos de propiedades indemostrables o contradictorias, como la hipótesis del continuo o la existencia de un cardinal inaccesible. Por esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica matemática.

El desarrollo histórico de la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas «puras» del infinito en la segunda mitad del siglo XIX, precedido por algunas ideas de Bernhard Bolzano e influenciado por Richard Dedekind. El descubrimiento de las paradojas de la teoría cantoriana, de conjuntos, formalizada por Gottlob Frege, propició los trabajos de Bertran Russell, Ernst Zermelo, Abraham Fraenkel y otros a principios del siglo XX.